Hydrodynamics¶
pyDeltaRCM approximates hydrodynamics through the use of a weighted random walk. See [1] and [2] for a complete description of hydrodynamic assumptions in the DeltaRCM model. In this documentation, we focus on the details of model implementation, rather than model design.
The water routing operations are orchestrated by route_water; the following sections narrate the sequence of events within a single call of this method.
Routing individual water parcels¶
Probabilities for water parcel routing to all neighbors and to self for each cell are computed once at the beginning of the water routing routine (get_water_weight_array called from run_water_iteration).
Water routing probability for a given cell \(j\) to neighbor cell \(i\) is computed according to:
where \(\mathbf{F}\) is the local routing direction and \(\mathbf{d_i}\) is a unit vector pointing to neighbor \(i\) from cell \(j\), and \(\Delta_i\) is the cellular distance to neighbor \(i\) (\(1\) for cells in main compass directions and \(\sqrt{2}\) for corner cells. \(R_i\) is a flow resistance estimated as an inverse function of local water depth (\(h_i\)):
The exponent \(\theta\) takes a value of unity by default for water routing (theta_water, Default Model Variable Values), leading to routing weight for neighbor cell \(i\):
These weights above are calculated only for wet neighbor cells; all dry neighbor cells take a weight value of 0 (_get_weight_at_cell_water).
Finally, probability for routing from cell \(j\) to cell \(i\) is calculated as:
Weights are accumulated for 8 neighbors and a probability of 0 is assigned to moving from cell \(j\) to cell \(j\) (i.e., no movement).
These 9 probabilities are organized into an array self.water_weights with shape (L, W, 9)`.
The following figure shows several examples of locations within the model domain, and the corresponding water routing weights determined for that location.
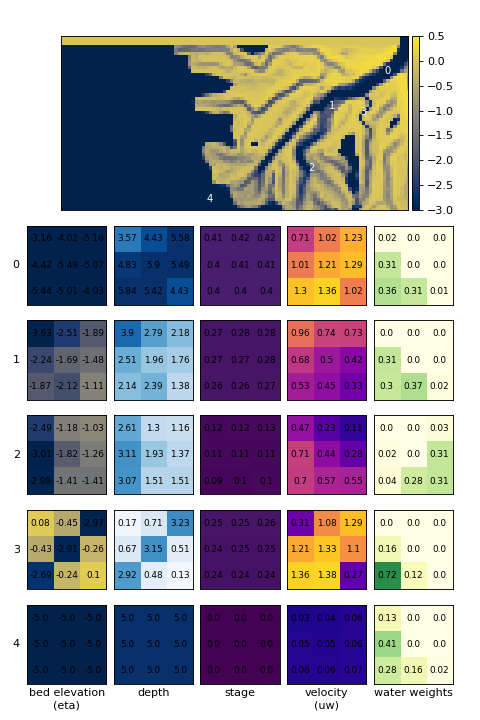
Because probabilities are computed for all locations once at the beginning of water iteration, all water parcels can be routed in parallel step-by-step in run_water_iteration.
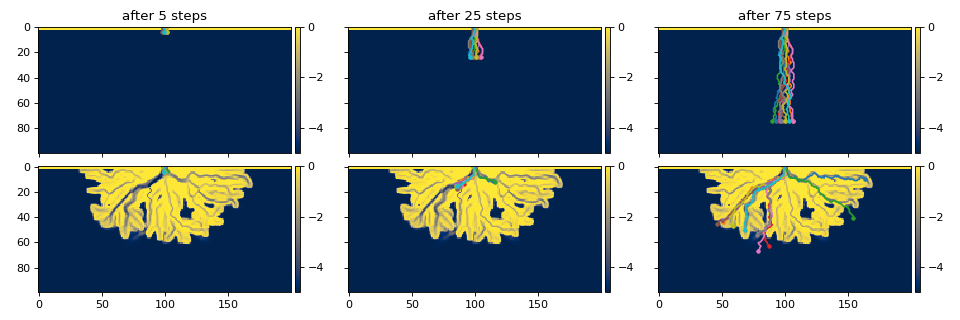
During iteration, the direction of the random walk is chosen for each parcel via _choose_next_directions, which internally uses random_pick() for randomness.
For example, see the random walks of several parcels below:
Todo
add sentence or two above about check_for_loops.
Water routing completes when all water parcels have either 1) reached the model domain boundary, 2) taken a number of steps exceeding stepmax, or 3) been removed from further routing via the _check_for_loops function.
Combining parcels into free surface¶
Following the routing of water parcels, these walks must be converted in some meaningful way to a model field representing a free surface (i.e., the water stage).
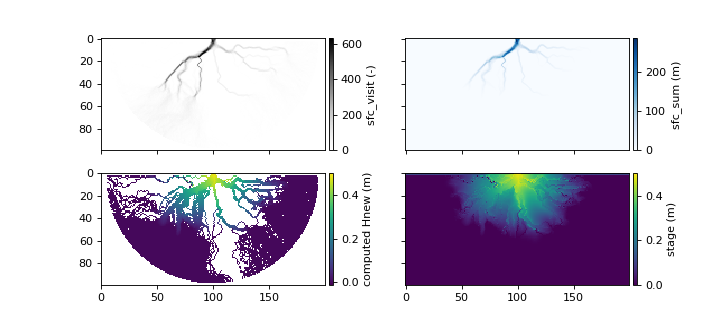
First, the compute_free_surface() is called, which takes as input the current bed elevation, and the path of each water parcel (top row in figure below).
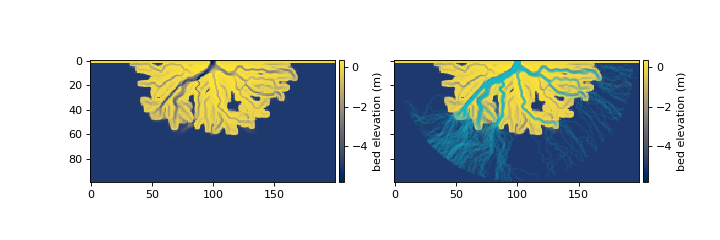
The compute_free_surface() method internally calls the _accumulate_free_surface_walks() function to determine 1) the number of times each cell has been visited by a water parcel
(sfc_visit), and 2) the total sum of expected elevations of the water surface at each cell (sfc_sum).
_accumulate_free_surface_walks() itself iterates through each water parcel, beginning from the end-point of the path, and working upstream; note that parcels that have been determined to “loop” (_check_for_loops() and described above) are excluded from computation in determining the free surface.
While downstream of the land-ocean boundary (determined by a depth-or-velocity threshold), the water surface elevation is assumed to be 0, whereas upstream of this boundary, the predicted elevation of the water surface is determined by the distance from the previously identified water surface elevation and the background land slope (S0), such the the water surface maintains an approximately constant slope for each parcel pathway.
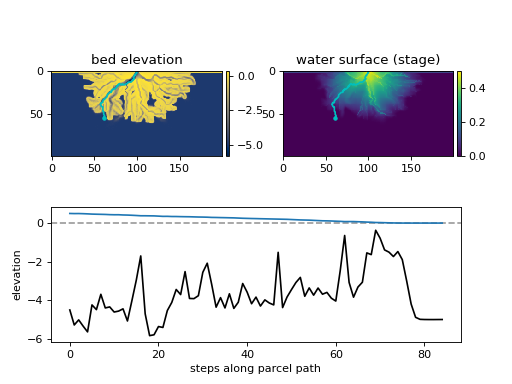
The algorithm tracks the number of times each cell has been visited by a water parcel (sfc_visit), and the total sum of expected elevations of the water surface at each cell (sfc_sum), by adding the predicted surface elevation of each parcel step while iterating through each step of each parcel.
Next, the output from _accumulate_free_surface_walks() is used to calculate a new stage surface (H_new) based only on the water parcel paths and expected water surface elevations, approximately as H_new = sfc_sum / sfc_visit.
The updated water surface is combined with the previous timestep’s water surface and an under-relaxation coefficient (omega_sfc).
With a new free surface computed, a few final operations prepare the surface for boundary condition updates and eventually being passed to the sediment routing operations (inside finalize_free_surface()).
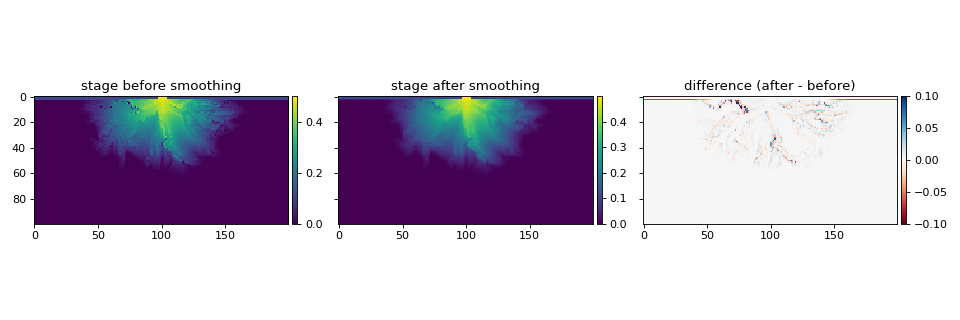
A non-linear smoothing operation is applied to the free surface, whereby wet cells are iteratively averaged with neighboring wet cells to yield an overall smoother surface.
The smoothing is handled by _smooth_free_surface() and depends on the number of iterations (Nsmooth) and a weighting coefficient (Csmooth).
Finally, a flooding_correction() is applied to the domain.
In this correction, all “dry” cells (a cell where the flow depth is less than the dry_depth) are checked for any neighboring cells where the water surface elevation (stage) is higher than the bed elevation of the dry cell.
If this condition is met for a given dry cell, the dry cell is flooded: the stage of the dry cell is set to the maximum stage of neighboring cells.
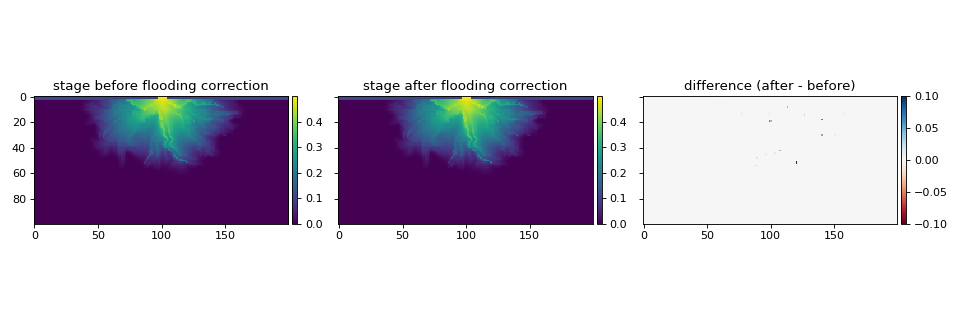
Similar to _smooth_free_surface() described above, flooding_correction() acts to remove roughness in the water surface and contributes to model stability.
Finalizing and boundary conditions to sediment routing¶
The final step of the water routing operations in each call to route_water is the updating of model fields, and application of a few corrections and boundary conditions.
These operations are handled within finalize_water_iteration.
First, the stage field is limited to elevations above or equal to sea level H_SL. Then, the depth field is updated as the vertical distance between the stage field and the bed elevation eta. These operations ensure that these fields are in agreement over the entire model domain.
Next, methods update_flow_field and update_velocity_field are called, which handle the updating of water discharge and water velocity fields, respectively.
Note
The next step in the model update sequence is sediment routing (route_sediment). For more information on the next stage, see Morphodynamics.