deltametrics.plan.compute_shoreline_roughness

deltametrics.plan.compute_shoreline_roughness(shore_mask, land_mask, **kwargs)

Compute shoreline roughness.

Computes the shoreline roughness metric:

\[L_{shore} / \sqrt{A_{land}}\]

given binary masks of the shoreline and land area. The length of the shoreline is computed internally with compute_shoreline_length.

Parameters:

• shore_mask (ShorelineMask, ndarray) – Shoreline mask. Can be a ShorelineMask object, or a binarized array.

• land_mask (LandMask, ndarray) – Land mask. Can be a LandMask object, or a binarized array.

• **kwargs – Keyword argument are passed to compute_shoreline_length internally.

Returns:

roughness – Shoreline roughness, computed as described above.

Return type:

float

Examples

Compare the roughness of the shoreline early in the model simulation with the roughness later. Here, we use the elevation_offset parameter (passed to ElevationMask) to better capture the topography of the pyDeltaRCM model results.

golf = dm.sample_data.golf()

# early in model run
lm0 = dm.mask.LandMask(
    golf['eta'][15, :, :],
    elevation_threshold=0,
    elevation_offset=-0.5)
sm0 = dm.mask.ShorelineMask(
    golf['eta'][15, :, :],
    elevation_threshold=0,
    elevation_offset=-0.5)

# late in model run
lm1 = dm.mask.LandMask(
    golf['eta'][-1, :, :],
    elevation_threshold=0,
    elevation_offset=-0.5)
sm1 = dm.mask.ShorelineMask(
    golf['eta'][-1, :, :],
    elevation_threshold=0,
    elevation_offset=-0.5)

Let’s take a quick peek at the masks that we have created.

fig, ax = plt.subplots(1, 2, figsize=(8, 3))
lm0.show(ax=ax[0])
sm0.show(ax=ax[1])
plt.show()

(png, hires.png)

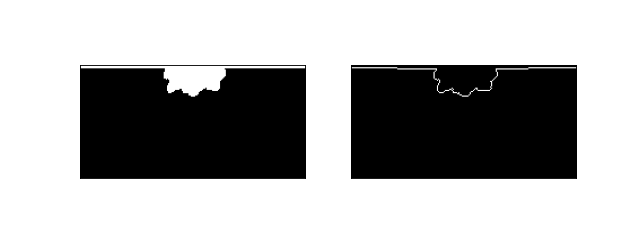
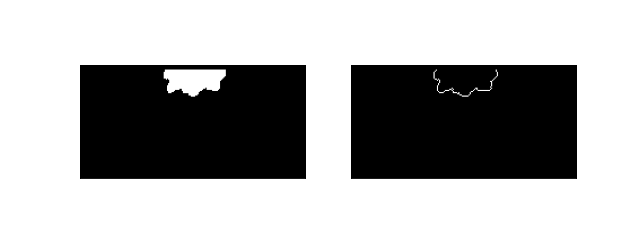
In order for these masks to work as expected in the shoreline roughness computation, we need to modify the mask values slightly, to remove the land-water boundary that is not really a part of the delta. We use the trim_mask() method to trim a mask.

lm0.trim_mask(length=golf.meta['L0'].data+1)
sm0.trim_mask(length=golf.meta['L0'].data+1)
lm1.trim_mask(length=golf.meta['L0'].data+1)
sm1.trim_mask(length=golf.meta['L0'].data+1)

fig, ax = plt.subplots(1, 2, figsize=(8, 3))
lm0.show(ax=ax[0])
sm0.show(ax=ax[1])
plt.show()

(png, hires.png)

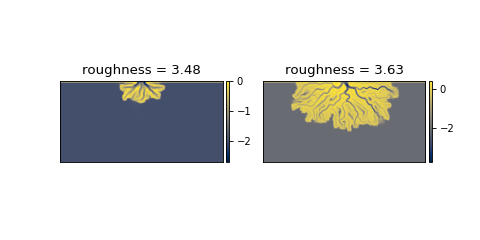
And now, we can proceed with the calculation.

# compute roughnesses
rgh0 = dm.plan.compute_shoreline_roughness(sm0, lm0)
rgh1 = dm.plan.compute_shoreline_roughness(sm1, lm1)

# make the plot
fig, ax = plt.subplots(1, 2, figsize=(6, 3))
golf.quick_show('eta', idx=15, ax=ax[0])
ax[0].set_title('roughness = {:.2f}'.format(rgh0))
golf.quick_show('eta', idx=-1, ax=ax[1])
ax[1].set_title('roughness = {:.2f}'.format(rgh1))
plt.show()

(png, hires.png)