deltametrics.plan.compute_shoreline_length

deltametrics.plan.compute_shoreline_length(shore_mask, origin=[0, 0], return_line=False)

Compute the length of a shoreline from a mask of the shoreline.

Algorithm attempts to determine the sorted coordinates of the shoreline from a ShorelineMask.

Warning

Imperfect algorithm, which may not include all True pixels in the ShorelineMask in the determined shoreline.

Parameters:

• shore_mask (ShorelineMask, ndarray) – Shoreline mask. Can be a ShorelineMask object, or a binarized array.

• origin (list, np.ndarray, optional) – Determines the location from where the starting point of the line sorting is initialized. The starting point of the line is determined as the point nearest to origin. For non-standard data configurations, it may be important to set this to an appropriate value. Default is [0, 0].

• return_line (bool) – Whether to return the sorted line as a second argument. If True, a Nx2 array of x-y points is returned. Default is False.

Returns:

• length (float) – Shoreline length, computed as described above.

• line (np.ndarray) – If return_line is True, the shoreline, as an Nx2 array of x-y points, is returned.

Examples

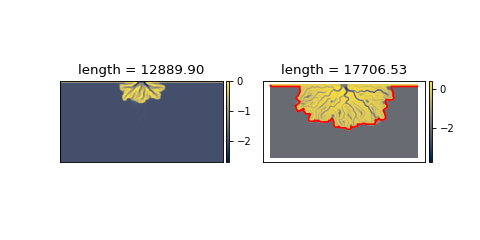
Compare the length of the shoreline early in the model simulation with the length later. Here, we use the elevation_offset parameter (passed to ElevationMask) to better capture the topography of the pyDeltaRCM model results.

golf = dm.sample_data.golf()

# early in model run
sm0 = dm.mask.ShorelineMask(
    golf['eta'][15, :, :],
    elevation_threshold=0,
    elevation_offset=-0.5)

# late in model run
sm1 = dm.mask.ShorelineMask(
    golf['eta'][-1, :, :],
    elevation_threshold=0,
    elevation_offset=-0.5)

# compute lengths
len0 = dm.plan.compute_shoreline_length(sm0)
len1, line1 = dm.plan.compute_shoreline_length(sm1, return_line=True)

# make the plot
fig, ax = plt.subplots(1, 2, figsize=(6, 3))
golf.quick_show('eta', idx=15, ax=ax[0])
ax[0].set_title('length = {:.2f}'.format(len0))
golf.quick_show('eta', idx=-1, ax=ax[1])
ax[1].plot(line1[:, 0], line1[:, 1], 'r-')
ax[1].set_title('length = {:.2f}'.format(len1))
plt.show()

(png, hires.png)